工程问题在行测数学运算是一种重要的题型，经常会考到，尤其是交替合作完工问题。并且有负效率参与的合作完工更是难点，其实这种题型是有一定规律的，即有明确的解题步骤，也是一种模型即青娃跳井模型，掌握这一模型之后能够快速的解题。现就给广大考生讲解青蛙跳井模型高效解决这类问题，希望能够帮助到大家。

　　一、题型特征：

　　有方向相反的单位量，循环完成总工作。

　　二、模型建立：

　　母题：现有一口深20米的井，有一只青蛙坐落于井底，青蛙每次跳的高度为5米，由于井壁比较光滑，青蛙每跳5米下滑3米，这只青蛙跳几次能跳出此井?

　　解析：青蛙向上跳5米，接下来下滑3米，这个过程看作一个周期即周期为1次，在这个周期内总共向上跳了2米(即为周期内任务量)，同时向上跳的最大高度为5米(即为周期峰值)。由于青蛙最后一定是在向上跳时跳出井的，同时为了更快的跳出，为了保证最后无论剩余多少都能保证一次跳出，所以预留最大高度5米。然后求需要的整周期数

　　1、三个基本数据：

　　(1)周期数：循环一次所用的时间;

　　(2)周期内工作量：周期内任务累积的总工作量;

　　(3)周期峰值：周期内任务累积的最大值。

　　2、操作步骤：

　　(1)根据题目已知条件，确定三个基本数据，预留周期峰值，求出整周期数;

　　(2)工作余量的具体处理;

　　(3)根据题目问法，计算出所求量的具体值

　　三、应用

　　工程问题-有负效率参与的交替合作问题

　　例题：某游泳馆内有甲丙两个进水管和乙丁两个排水管，单开进水管向空池注水，甲需3小时，丙需5小时;单开排水管将满池的水放空，乙需4小时，丁需6小时，现池内有,的水，如果按照甲、乙、丙、丁的顺序轮流各开一个小时，那么经过多少小时后水池的水开始溢出?

　　4.5小时 15 分钟

　　B.10 小时 45分钟

　　C.15 小时 15 分钟

　　D.20 小时 45分钟

　　解析:答案为 D。

　　第一步:确定三个基本数据，预留周期峰值，求整周期数。根据题目问法求时间，存在乘除关系且工作总量是个不变量且具有任意性，想到用特值法，列表法

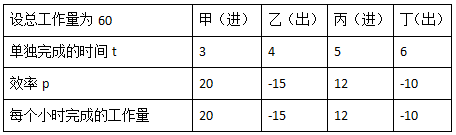
　　分别求出周期任务量为7、周期峰值20和周期4小时，从而求出周期数

　　第二步:任务余量的具体处理，

　　第三步:求总时间。

　　本文主要是讲青蛙跳井问题的题型特征和模型的建立，以及它在工程问题中的应用。重点掌握青蛙跳井模型的题型特征，知道何时用这种模型，接下来要知道它的具体操作步骤，重点是周期峰值的预留求出整周期数和任务余量的具体处理，这是两个很关键的步骤，希望同学们能够理解，并通过题目练习，这样才能熟能生巧，快速解题。